贝塞尔曲线的升阶

一条二次贝塞尔曲线能否转换成对应的三次贝塞尔曲线，并且两条曲线严格重合（而不是拟合）？

我看到这个问题的第一反应：“把中间的控制点复制一份不就行了嘛”，但仔细一想细思恐极似乎哪里不对。事实上，这样做相当于改变了控制点的权重，会将曲线“吸”向控制点。

直觉告诉我，这个问题的答案虽然不能想当然，但应该是可行的。于是自己动笔，丰衣足食。

贝塞尔曲线的性质

从定义讲起。贝塞尔曲线是一种借助若干个控制点定义的参数曲线。由n+1个控制点定义的贝塞尔曲线称为n次贝塞尔曲线。我们在绘图软件中经常会看到它，例如Windows的“画图”工具中的曲线，就是一条三次贝塞尔曲线。

以三次贝塞尔曲线为例，令控制点为P0、P1、P2、P3。我们定义一个0到1之间的参数t，将直线P0-P1划分为t:(1-t)的两部分，令分界点为Q01，同理得到Q12和Q23；再划分Q01和Q12得到R02，同理得到R13；最后划分R02和R13得到S，这就是贝塞尔曲线上的一个点。取遍所有t得到的点S的集合，即可得到一条贝塞尔曲线。

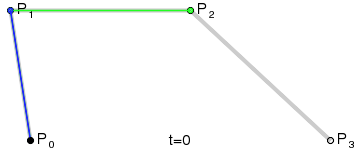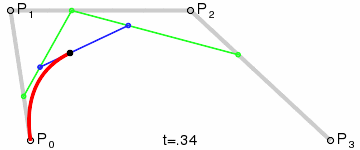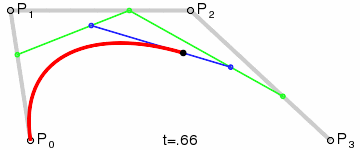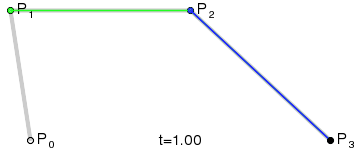
我们很容易发现，贝塞尔曲线上的任意一个点都是控制点的线性组合，每个点的坐标都可以表达为：

B(t)=k0*P0+k1*P1+k2*P2...+kn*Pn，其中k0+k1+k2...+kn=1

（事实上，系数是：ki=nCi*t^(n-i)*(1-t)^i）

因此，我们可以对贝塞尔曲线和它的控制点进行线性变换（更进一步地，进行放射变换），得到的新曲线就是由变换后的控制点定义的贝塞尔曲线。

二次转三次

//注：将本节内容脑补为cosplay的请自行面壁。

首先，考虑到贝塞尔曲线可以和控制点一起进行线性变换，我们可以通过线性变换和平移，使二次贝塞尔曲线的三个控制点位于(1,0)、(0,0)和(0,1)。

那么，这条二次贝塞尔曲线就是：

B2(t)=(1,0)*t^2+(0,1)*(1-t)^2

也就是说：

x=t^2

y=(1-t)^2

然后我们考虑对应的三次贝塞尔曲线。

由于第二个和倒数第二个控制点分别决定了曲线在两个端点处的切线方向（读者可以动笔验证一下，这对于绘图软件来说是一个非常有用的性质），要让两条曲线重合，这两个控制点必须分别在直线y=0和x=0上。

再考虑到函数图像和控制点关于y=x对称，我们可以令四个控制点分别为：(1,0)、(a,0)、(0,a)、(0,1)。

得到曲线的表达式：

B3(t)=（1,0)*t^3+(a,0)*3t^2*(1-t)+(0,a)*3t*(1-t)^2+(0,1)*(1-t)^3

代入曲线上的一个点(1/4,1/4)，求得a=1/3。

因此三次贝塞尔曲线的控制点为(1,0)、(1/3,0)、(0,1/3)、(0,1)，有：

x=t^3+t^2*(1-t)=t^2

y=(1-t)^3+(1-t)^2*t=(1-t)^2

和二次贝塞尔曲线的表达式完全相同，可知它们是重合的。

再考虑变换，任意的二次贝塞尔都可以用相同的方式转换成三次贝塞尔曲线。只需要在相邻控制点（P0与P1、P1与P2）之间的连线上，靠近中间控制点（P1）的1/3处取新的控制点就可以了。

推广

升阶同样适用于更高阶的贝塞尔曲线。

考虑从n阶升到n+1阶。

由于Bi=Bi*t+Bi*(1-t)，我们可以将贝塞尔曲线的表达式代入，并将关于t的部分提取出来。令新曲线的第i个点为P，原曲线的第i-1个点为Q，第i个点为R：

k'i*P=k'i*i*Q/(n+1)+k'i*(n+1-i)*R/(n+1)

因此：

P=i/(n+1)*Q+(n+1-i)/(n+1)*R

我们可以进一步推出，从n阶升到n+r阶的公式是：

P=sum(Pj*nCj*rC(i-j)/(n+r)Ci)